Страница программы NumLock Calculator
ИНСТРУКЦИЯ
ПО ПРОГРАММИРОВАНИЮ NL.
Решение
задач сопромата
Калькулятор,
который мне посчастливилось создать, помогает людям считать - в самых разных задачах,
которые ставит реальная жизнь, даже в тех, до которых я бы сам никогда бы не додумался.
В этом тексте, написанном моим давним пользователем и критиком Оконечниковым А.Н., дается пример решения такой задачи – задачи сопромата. Подробное пошаговое руководство может служить образцом дотошного отношения к делу, в нем используются все возможности программы, о некоторых из которых ее автор и не подозревал J .
Прежде, чем вы начнете работать с этим текстом, скачайте пожалуйста файл sopromat.zip и прочитайте readme
Постановка
задачи и начало программирования
Пусть
перед нами стоит следующая задача: балка лежит на двух опорах. Профиль балки -
швеллер, сваренный из полосового материала. Никаких нагрузок, кроме собственного
веса, балка не несет. Необходимо определить:
Схема
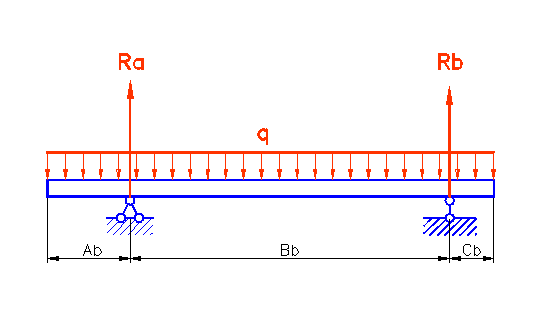
нагружения балки представлена на рис.1.Сечение балки - на рис. 2.

Рис.1
Материал
балки - сталь.
С
точки зрения программирования мы должны составить программу таким образом, чтобы
все вычисления проводились, по возможности, без нашего дополнительного вмешательства,
чтобы вводимые и выводимые данные были правильны и понятны, а составленные формулы
могли бы быть использованы для других расчетов, то есть были бы, по возможности,
универсальными.
Определим
исходные данные и константы, которые будут нам необходимы для решения задачи.
Отметим для себя, что для того, чтобы промежуточные и окончательные результаты вычислений были правильными, надо внимательно следить за всеми размерностями в составляемых нами формулах.
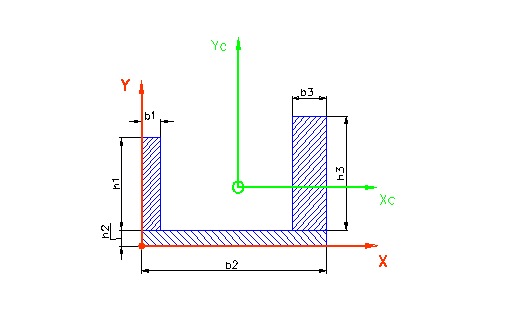
Рис.2
Определим
количество вводимых исходных данных: 3 сечения имеют по 2 размера = 6, размеры
балки и расстояния до опор: 3, 2
"константы", которые тоже могут быть переменными (при изменении материала
балки). Итого 11 исходных данных.
Как
известно, в NL имеются следующие возможности ввода и вывода данных: в строке ввода
(списки, разделяющиеся точкой с запятой - только для ввода), из ячеек памяти (их
всего 10 - с 0 по 9, каждая из которых допускает ввод и вывод списков, но только
вручную), с помощью временных переменных m0-m99 (всего 100 ячеек, которые допускают
ввод и вывод только одиночных данных), но которые можно использовать и в программном
режиме.
Еще
одна особенность NL, которая состоит в том, что для вывода результатов при использовании
строки ввода данных необходимо каждый раз вводить эти исходные данные, а при использовании
временных переменных m, доступ одновременно ко всем
вводимым данным отсутствует.
Попробуем
сначала решить задачу без использования ячеек памяти и временных переменных. Две
"константы" для облегчения принимаем равными соответствующим константам
для стали.
Прежде,
чем перейти к программированию необходимо задать конкретные названия всем исходным
данным. Пусть h1, b1 ,h2 ,b2 ,h3 ,b3 - это
высоты и ширины соответственно левой, средней и правой полос сечения. Ab,
Bb, Cb - соответственно расстояния от левого конца балки до левой опоры, между
опорами и от правой опоры до правого конца балки. Все буквы - латинские (они могут
быть любыми, но мы будем использовать только латинские).
Теперь
дадим названия выходным данным. Ra, Rb - реакции левой и правой опор. Ixcост_шв
- момент инерции составной балки относительно главной оси. Y0 - прогиб
левого конца балки, Fi0 - угол говорота левого конца балки. Mmax
- максимальный изгибающий момент. Snmax - максимальные нормальные
напряжения.
Константы:
Pst=7.85E-6 - плотность стали, кг/мм3, Est=2E6 - модуль упругости
стали, кг/см2.
Все
остальные промежуточные переменные и результаты будем описывать в процессе решения
задачи.
Для
записи формул создадим (в папке Функции, ее можно открыть через меню Пуск/Программы/NumLock
Calculator
3.2) новый текстовый файл с расширением
.udf, например, Балка.udf. (Проще всего для этого скопировать существующий
файл, например Константы.udf
переименовать его и вычистить из копии старое содержимое - там всего пара строк)
Для
записи констант создадим новый файл, с тем же расширением, но назовем его "Постоянные.udf".
Это сделано для того, чтобы не "портить" основные файлы папки NL / Функции.
То, что пишется (или уже было написано) непосредственно в файлы калькулятора или
в его строку вычислений будем выделять синим цветом.
Для констант запишем в файле Постоянные.udf:
Pst=7.85E-6
//Плотность стали, кг/мм3
Все
остальные формулы будем записывать в файле Балка.udf.
Возьмем
все необходимые формулы из теории
сопротивления материалов (всем, кому интересно, откуда все эти формулы взялись
советуем обратиться к специальной литературе, поскольку наша задача - это изложить
программирование на NL, а не основы сопромата).
Ra=0.5*q*((Bb+Ab)^2+Cb^2)/Bb,
или
Здесь можно использовать любую формулу. Мы используем вторую, и одновременно покажем каким образом создавать связанные формулы.
q=Ssum*Pst
q
- это величина распределенной нагрузки. Эта переменная выбрана пока для удобства
записи (чтобы формулы были короче). По условиям задачи q зависит от сечения
балки и плотности выбранного материала.
Ssum
- это суммарное сечение балки.
Из этих формул следует, что для вычисления реакций опор достаточно использовать расстояния до опор и суммарное сечение балки.
Будем пока считать, что общее сечение балки известно, например, что оно равно 200см2.
Запишем
(в файл Балка.udf)
наши формулы в следующем виде:
Rb(Ab;Bb;Cb;Ssum)=0.5*q*((Bb+Cb)^2-Ab^2)/Bb
Обратите
внимание на следующее. У нас появилась новая функция: Rbb. Эта функция
является той же самой, что и Rb, только без ввода исходных данных. Таким
образом, если мы вычисляем Ra (с вводом списка данных), то вычисляется
q, затем складываются Ab+Bb+Cb, затем вычисляется Rbb по
второй формуле с использованием исходных данных, а затем выводится правильный
результат. Если в третьей формуле использовать не Rbb, а Rb, то
будет выдано сообщение об ошибке, поскольку Rb работает только как самостоятельная
функция, то есть в связке она использоваться не может. Rbb является связанной
функцией и может быть использована в любой (!) пользовательской формуле в
качестве аргумента! (Нужно только чтобы в той пользовательской формуле, с которой
осуществляется связь, задавались аргументы, необходимые для Rbb)
В
четвертой формуле появился множитель 100, который служит лишь для согласования
размерности (1см2=100мм2), поскольку плотность мы договорились брать в кг/мм3,
а площадь - в см2. Результат, т.е значение реакций будет получаться, соответственно
в кг. Ну а Ab, B, и Cb мы договорились брать в миллиметрах. Если
интересно, то попробуйте подсчитать общий вес балки. Его можно подсчитать как
q*(Ab+Bb+Cb) - это у нас уже встречалось в третьей формуле, только мы отдельно
функцию не записывали. Или как сумму реакций опор, т.е. Ra+Rb.
Ну,
хорошо. Формулы составили, а считать - то как? Сейчас разберемся. Тут нужен доступ
к кнопкам калькулятора, чтобы было на что нажимать для
вывода результатов вычислений на дисплей. (Возможно, конечно просто
«вручную» набить и вычислить формулы
в окошке вычислений, но мы же договорились автоматизировать все, что возможно?)
Кнопки
и переключатели NL
Давайте ознакомимся поподробнее с кнопками NL. Выберите в калькуляторе вид под названием "Инженерный". Большинство кнопок на панели NL функциональные, то есть при их нажатии вы видите на дисплее или число или оператор или название функции со скобкой или без нее. Особое положение и назначение имеют кнопки-переключатели. Это кнопки [Inv] и [Hyp]. При их нажатии происходит небольшое изменение внешнего вида и вместо одних названий функциональных кнопок появляются другие. Таким же образом происходит "расширение" возможностей NL, дополнение его интерфейса новыми функциональными кнопками и кнопками-переключателями.
Выберите
теперь вид «Конструктор». Вы видите внизу панели NL раздел «Пользовательские функции»
и «Библиотеки». Кнопки в первом разделе
- это переключатели, которые будут вызывать новые функциональные кнопки.
Обратите внимание на кнопки [Вычисления1] и [reserv2] – [reserv7]. Пока нажатие
на них не вызывает никаких действий - это будут наши первые переключатели и функциональные
кнопки для решения этой задачи.
Откройте
для редактирования в любом текстовом редакторе файл с названием
"Конструктор.itf". (Пуск-Программы-NumLock
Calculator
3.2-Виды). Найдите
в разделе "КНОПКИ ДОПОЛНИТЕЛЬНЫХ ПЕРЕКЛЮЧАТЕЛЕЙ"
кнопку
под названием
[btSwitch8]
и
замените написанное там на следующее:
Caption=Балка
Visible=1
Top=325
Left=7
Height=20
Width=101
Tag=1
Font=MS Sans Serif,B,8
Hint=Расчет балки
Далее
в конце файла найдите раздел "ФУНКЦИИ ПЕРЕКЛЮЧАТЕЛЕЙ"
а в разделе
напишите
;[Балка]
reserv7=Rb
reserv6=Ra
Мы
сделали следующее. На кнопку-переключатель с номером 8 поместили новое название
"Балка", а в подсказке к этой кнопке сделали пояснение "расчет
балки". Далее, мы зарезервировали функциональные кнопки, которые в режиме
по умолчанию имели заголовки [reserv7] и [reserv6], и задали им выполнение пользовательских
функций Ra и Rb.
Сохраните
файл. Формулы, которые мы составляли ранее, должны быть также записаны в файл
«Балка.udf», а константы - в «Постоянные.udf», а сами файлы сохранены. Обратите
внимание, что папки для файлов udf и itf должны быть соответственно «Функции»
и «Виды». Теперь снова загрузите вид "Конструкторский". На месте кнопки
[Вычисления2] появилась кнопка [Балка]. Нажмите на эту кнопку. Вместо кнопок [reserv7]
и [reserv6] Вы видите теперь кнопки, обозначенные [Rb] и [Ra]. Все правильно.
Давайте
теперь попробуем что-нибудь вычислить. Для этого вводим исходные данные, например,
1000;1000;1000;200 и нажимаем на кнопку
[Rb]. На экране:
Rb(1000;1000;1000;200) = 235,5.
Мы
ввели расстояния между опорами и от опор до концов балки по 1 м и выбрали площадь
сечений составного швеллера равным 200см2. Получили реакцию опоры В=235.5
кг. Чтобы снова не набирать исходные данные вручную, нажмите два раза на клавиатуре
РС клавишу NL. На экране - снова наши исходные данные. Нажимаем теперь кнопку
[Ra]. На экране:
Ra(1000;1000;1000;200) = 235,5.
То же самое! Балка-то лежит симметрично, значит и реакции опор одинаковые. А сами
реакции подсчитаны правильно? Проверим сначала правильно ли подсчитан вес балки.
Открываем справочник по стандартным швеллерам. К сожалению стандартных швеллеров
с площадью поперечного сечения 200см2
нет. Находим самый большой. Это №40. Площадь поперечного сечения 61.5см2. Наш
больше в 200/61.5 = 3,252032520325
раза. Вес погонного метра у стандартного 48.3. Наш же длиннее ровно в 3 раза.
Умножаем 3,252032520325*48,3
*3 = 471,2195121951. А реакция
опор при таком же расположении была бы 471.2195121951/2 = 235,6097560976.
Значит реакции опор мы подсчитали правильно. А если сдвинуть опоры? Например,
Ra(0;1000;1000;200) = 0. Интересный
результат. Все понятно. Вся нагрузка приходится на опору В. Балка "повисла"
на этой опоре и на опору А не давит. Чуть-чуть изменим длину Ab:
А
если увеличить Ac?
Ra(0;1000;1001;200) = -0,1570785???
Отрицательная
реакция? Ничего страшного не произошло. Просто мы вышли из области допустимых
значений аргументов составленных нами функций. То, что мы записали в исходных
данных должно фактически означать, что балка начала вращаться вокруг оси B, что
не соответствует условию задачи о том, что балка лежит на двух опорах. Поэтому
впредь будем внимательны при вводе исходных данных.
Теперь, после того как мы убедились в том, что формулы являются вполне работоспособными, напишем подсказку: что это такое и чем его едят. Откроем файл с нашими формулами и запишем так:
Rb(Ab;Bb;Cb;Ssum)=0.5*q*((Bb+Cb)^2-Ab^2)/Bb
// Реакция опоры В, кг (расстояния: лев.край-лев.опора, мм; между опорами,
мм; прав.край-прав.опора, мм; Сум.сечение,см2). Здесь
формула от подсказки отделяется //, а дальше пишется
все, что надо знать при использовании формулы: результат, аргументы,
размерности, разделители списков и т.д.
То есть все то, что необходимо для удобного пользования каждой формулой.
А
как же быть с суммарным сечением? Теперь придется заняться геометрическими характеристиками
сечений. Для расчета балок, подвергающихся изгибу, обычно используются следующие
геометрические характеристики: площадь, статический момент, положение центральных
осей, момент инерции, момент сопротивления. Все эти характеристики взаимосвязаны,
поэтому, определяя их (а это нам тоже нужно), мы, естественно определим и суммарное
сечение.
В
файле Брус.txt приведены
уже готовые формулы (без математических выводов), которые мы и будем использовать.
Для порядка скажу только, что за исходные координатные оси были выбраны ось ординат,
проходящая по нижней стороне среднего сечения, и ось абсцисс, проходящая по через
центр нижней стороны. Т.е. была соблюдена вертикальная симметрия.
Скопируйте
весь раздел с формулами геометрических характеристик в Ваш файл «Балка.udf» (Внимание!
При копировании функций нужно знать: калькулятор не загрузится, если встретит
функции с одинаковыми именами)
Теперь
посмотрим, какие данные необходимо вводить для расчета геометрических характеристик
нашего сечения. Их шесть (по три ширины и по три высоты). Все они должны записываться
в строку ввода через точку с запятой. Добавим 3 параметра, связанные с длиной
балки. Итого 9. Ввод в одну строку будет довольно неудобным, а подсказка получится
слишком длинной. Да и задача еще не решена до конца. Впереди ведь еще вычисление
моментов, напряжений и прогибов. Поэтому все-таки нам придется использовать сохранение
промежуточных значений. Как мы уже знаем хранить данные можно в ячейках памяти
или как временные переменные. Попробуем для этого использовать временные переменные
m0 - m99.
При этом желательно обеспечить следующий алгоритм. Вычисление какого-то параметра,
который необходим для последующих вычислений, сохранение его в памяти, затем при
вызове очередной формулы, обращение непосредственно за данными в нужную ячейку,
запись результата (при необходимости) в следующую ячейку и т. д. К сожалению,
эту операцию полностью автоматизировать мы не сможем. NL не умеет последовательно
исполнять две несвязанные функции, т.е. нельзя записать последовательно выполнение
функции вычисления значения и присвоения этого значения временной переменной.
Поэтому операцию сохранения в памяти придется
выполнять вручную.
Сначала
определим те параметры, которые нам надо "запомнить" для того, чтобы
довести решение до конца. А перед этим попытаемся до конца решить задачу. Итак,
будем считать, что реакции опор найдены, и геометрические характеристики составного
сечения вычислены. Далее мы должны найти максимальные изгибающие моменты. Поскольку
схема расположения опор может быть не симметричной, то максимальный момент будет
вычисляться через расстояние Zm от левого
конца балки как
Mzm=Ra(Z0-Ab)-(qZ0^2)/2,
где Z0=Ra/q.
В
двух сечениях балки (в местах опор) также возникают большие изгибающие моменты,
поэтому запишем и их. Из трех значений моментов выберем наибольший.
MzA=(qAb^2)/2
Как
Вы видите, никаких новых аргументов у нас не появилось.
Максимальные
нормальные напряжения будут определяться как
Snmax=Mmax/Wxc,
где Wxc - момент сопротивления сечения. Он уже определен в геометрических
характеристиках и записан в файле «Балка.udf». Отметим для себя, что он нам нужен
и хорошо бы его "запомнить". Если Вы обратитесь к началу нашей задачи,
то таким же необходимым для "запоминания" параметром будет площадь поперечного
сечения.
Поехали
дальше. Осталось вычислить только угол поворота и прогиб балки на левом конце.
Мы даем набор пользовательских функций без объяснений. Пусть их теоретический вывод никого, кроме "сопроматчиков" не волнует.
Fi0=(((q(Ab+Bb)^4)/4!)-((RaBb^3)/3!)+((qAb^4)/4!))/E
Ixcост_шв Bb - это угол поворота.
Здесь
формула написана на привычном "математическом" языке, а не на языке
NL. При записи формул в файл необходимо соблюдать соответствующие правила. Относительно
количества скобок можно сказать, что лучше поставить "лишнюю" скобку,
чем не написать нужную. Кроме того, большинство записей с "лишними"
скобками смотрятся и редактируются гораздо проще.
Y0=((qAb^4)/4!E
Ixcост_шв)-Fi0Aa. - это искомый прогиб.
В
целом задача решена.
Обратите
внимание на то, что здесь, наконец, появился модуль упругости E
(мы о нем уже вспоминали в самом начале) и параметр Ixс, который,
к счастью является геометрической характеристикой сечения и уже вычислен. Его
тоже надо было бы запомнить после вычисления. Значит всего необходимо "запомнить"
3 промежуточных параметра, которые являются геометрическими характеристиками сечения.
Заменим
во всех формулах, где функцию суммарного сечения используется как аргумент на
переменную m1, Ixcост_шв - на
m2, Wxc - на m3.
Если Вы все выполнили правильно, то у Вас должно получиться так же, как в файле
«Брус.txt».
В этом файле описаны все функции, которые мы вместе составляли (Вы заметили,
что описания ранее введенных функций реакций опор стали зависеть уже всего от
трех аргументов?)
Теперь
необходимо оформить те кнопки, которые будут отвечать за сохранение промежуточных
результатов и одновременно закончить с кнопками .
Сначала
открываем файл «Балка.udf», который Вы начали создавать, и запишем туда три функции
присвоения временным переменным значений, которые находятся в строке ввода:
Func1(X)=m1:=X
// Занести суммарное сечение, см2
Func2(X)=m2:=X // Занести момент инерции Ixc, см4
Сохраним
этот файл. Запомним названия функций и откроем файл «Конструктор.itf». Найдем
в разделе "ДАННЫЕ ПАМЯТИ" кнопку:
[btNumPad53]
Caption=F(1)
Hint=Это
F1
Function=F1
Visible=1
Top=283
Left=516
Height=20
Width=62
Tag=1
Font=MS Sans Serif,B,8
Для
нас будут важны три первые строчки. Лучше всего такие названия скопировать, чтобы
не ошибаться. Здесь ведь важна не только конкретная привязка названия, подсказки
и функции к Caption, Hint or Function, но и то, какие буквы были использованы:
латиница, кириллица или их сочетание. Перейдем
теперь в раздел "ФУНКЦИИ ПЕРЕКЛЮЧАТЕЛЕЙ" и найдем наш переключатель
№8.
Запишем в любом месте этого переключателя следующее:
F(1)=Sсеч
F1=Func1
Это F1=Занести
сечение швеллера в ячейку m1
F(2)=Ixc
F2=Func2
Это F2=Занести Ixс швеллера в ячейку m2
F(3)=Wxc
F3=Func3
Это F3=Занести Wxc швеллера в ячейку m3
Порядок
записи строк может быть любым. То, что пишется слева от знака равенства должно
в точности соответствовать тому, то желаете изменить. Справа от знака равенства
Вы должны написать там, где был Caption: то,
что хотите видеть на кнопке, Hint: то, что
желаете видеть во всплывающей подсказке, Function
- то, что вы записали в качестве исполняемых функций, то есть это наши функции
запоминания характеристик сечения. Названия кнопок и названия функций могут полностью
не совпадать. Названия функций на кнопках служат только для информации. Сохраните
файл и перезагрузите NL. Кстати, нажимать кнопку "Выход" в "Главном
меню" не обязательно. Достаточно выбрать в разделе "Главного меню"
вид "Конструктор" и у Вас будет произведена перезагрузка файла вида
и всех файлов udf. Нажмем на кнопку "Балка". Теперь в той области NL,
где буквы "ПАМЯТЬ" вместо букв F(1),
F(2) и F(3)
появились наши Sсеч, Ixc и Wxс. Напишем в строке ввода какое-нибудь число и нажмем
на кнопку Sсеч. В строке ввода все исчезло. Как проверить что у нас в памяти.
Вводим в строку: m1, нажимаем Enter (на клавиатуре PC) или = на панели NL и видим
на дисплее m1= и далее наше число. Это означает, что число попало в ячейку памяти.
Те же операции произведем с двумя другими кнопками и убедимся, что все работает.
Теперь остается только присвоить кнопкам на функциональной панели NL необходимые
для решения нашей задачи функции и приступить к решению конкретного примера.
Опять
откроем файл "Балка.udf" и найдем в разделе "ФУНКЦИИ ПЕРЕКЛЮЧАТЕЛЕЙ"
наш переключатель №8. Самыми первыми мы оформили кнопки для вычисления реакций
опор Ra и Rb. Какие еще кнопки нам нужны? 3 кнопки с вычислением
геометрических характеристик, максимальный момент, максимальное напряжение изгиба,
прогиб и угол поворота. Геометрические характеристики поместим в среднюю колонку,
а все остальное, кроме Mmax
- в левую.
s&qrt=Sсеч_шв
e&xp=Ixcост_шв
&10^=Wxс_шв
reserv5=Mmax
&cos=Snmax
&tan=Y0
cotan&g=Fi0
Сохраним
файл и перегрузим NL. Нажимаем кпопку "Балка". Теперь все кнопки "заряжены"
и находятся на тех местах, куда мы их определили. Слева - окончательные результаты
расчетов, в середине - геометрические характеристики сечения, справа - реакции
опор и максимальный момент.
Программирование
закончено. Можно приступать к решению задач.
В
строке ввода запишем 0;6000;0 и поместим
этот список в ячейку памяти (MS)
под номером 1. Это сделано для того, чтобы было удобнее вызывать параметры схемы
в строку ввода. В качестве составного швеллера принимаем швеллер, аналогичный
стандартному №40. Это мы делаем для того, чтобы проверить как правильно считает
геометрические характеристики наша программа. Запишем характеристики составного
сечения: 115-8;13,5;8;400;115-8;13,5
и разместим этот список в ячейку памяти (MS)
под номером 2. Нажимаем кнопку "Балка".
Вычисляем
геометрические характеристики.
Sсеч_шв(107;13,5;8;400;107;13,5) = 60.89 (см2)
Заносим
это значение в область временных переменных: кнопка [Sсеч]->m1.
[MR(2)]->
Ixcост_шв(107;13,5;8;400;107;13,5) = 779,3222909194
(см4)->[Ixc]->m2.
{MR(2)]->
Wxс_шв(107;13,5;8;400;107;13,5) = 93,08850176815
->[Wxc] (см3)->m3.
Сравним
полученные геометрические характеристики с характеристиками стандартного швеллера
из справочника. Они должны не очень сильно отличаться.
Площадь=61.5
см2, Iy=642
см4, Wy=73.4
см3. (значения взяты по оси Y, поскольку наш
профиль развернут на 90 градусов.
А
сейчас будет еще проще. Вызываем список данных из MR(1).
Вес шестиметрового куска швеллера №40 составляет:
48.3*6 = 289.8
кг. (где 48.3 - вес 1 погонного метра швеллера).
Итак,
мы убедились, что составленные нами формулы работают правильно. (небольшое
несовпадение цифр относится к наличию скруглений у профиля
стандартного швеллера)
Решим
еще одну задачу. Положим нашу балку на опоры симметрично относительно середины
балки. Расстояние между опорами теперь пусть будет равно 1м или 1000мм.
Rb(2500;1000;2500) = 143.39595
Ra(2500;1000;2500) = 143.39595
Mmax(2500;1000;2500) = 14937.078125
Snmax(2500;1000;2500) = 160.4610434294
Y0(2500;1000;2500) = -0.05159051108243
Fi0(2500;1000;2500) = 2.263274123957E-5
Как
видно из результатов реакции не изменились, максимальный изибающий момент и напряжения
стали существенно меньше, появился отрицательный прогиб на левом конце балки (концы
балки "провисли" вниз), знак угла поворота изменился на обратный.
Решение
задачи заняло несколько секунд.
Мы
меняли только размещение опор. А можно ли поменять размеры поперечного сечения?
Можно. Более того. Формулы геометрических составлены таким образом, что мы можем
"считать" не только швеллера, показанные на рис.2, но и другие профили.
Так, например, если мы составим список размеров сечений, где отсутствуют размеры
третьей полосы (то есть присутствуют их нулевые значения), то получим профиль
уголка буквой L.
Если нулевыми будут представлены две из трех полос, то геометрические характеристики
будут вычислены для одной единственной полосы. Причем, все характеристики будут
подсчитаны для центральных осей выбранного сечения.
Возьмем
металлическую полосу высотой 10 мм, шириной 50 мм и длиной 6 метров. Положим ее
на последнюю из выбранных нами схем опирания бруса.
0;0;10;50;0;0
- первый список;
Обратите
внимание на то, что значения напряжений стали значительно выше. Если их сравнить
с пределом текучести стали при растяжении (2500 кг/см2), то видно, что достаточно
приложить по концам полосы небольшие дополнительные силы (например, встать вдвоем
на края полосы), и она "потечет", то есть потеряет свои упругие свойства
и согнется.
Попробуем
в последнем примере заменить характеристики стали на характеристики стекла. Временно
меняем:
Est=500000
Pst=2.5E-6
И
тогда получим:
Snmax(2500;1000;2500) = 468.75
Это значение напряжение выше, чем временный предел прочности стекла (400 кг/см2), что говорит о том, что при данной схеме полоса стекла переломится под собственным весом.
В
конце файла Брус.txt
записаны функции вычисления налогов. Это примерный аналог тех формул, которые
Вы можете увидеть в виде Финансовый. Скопируйте эти файлы в Ваш рабочий файл Балка.udf и попробуйте
разобраться самостоятельно с действиями кнопок TAX…
при включении переключателя Финансовый в виде Конструктор.
Выводы
В
результате программирования исходной задачи мы получили доступ к решению целого
класса задач прикладной механики (сопротивления материалов). Хотелось бы обратить
внимание на следующее. Мы выполняли вычисления по нескольким направлениям. Первое
- это вычисления геометрических характеристик сечения (они не зависят ни от материала,
ни от расположения опор и длины балки). Второе - это вычисления, связанные с свойствами
материала балки, расположением опор и длины балки. Второе направление можно было
бы разделить еще на два: выбор материала и его характеристик и другое - то, которое
зависит от схемы нагрузки балки, материала и сечения. ТОЛЬКО ПОСЛЕДНЕЕ ИЗ НИХ
ЯВЛЯЕТСЯ ФУНКЦИЕЙ ДВУХ ПЕРВЫХ, А ПЕРВЫЕ ДВА ЯВЛЯЮТСЯ НЕЗАВИСИМЫМИ! Имеется в виду
следующее. Геометрические характеристики сечения могут быть вычислены независимо
от схемы нагрузки и исходных материалов. Материалы, естественно, зависят только
от нашего выбора. И только завершающие расчеты мы не можем провести без первых
двух. Таким образом, логично было бы для правильной организации библиотек создавать
независимые друг от друга блоки вычислений. Для такого узкого круга задач по сопромату,
как расчеты статически определимых систем (балок) такими библиотеками могут быть:
Уже сейчас NL позволяет программировать и решать очень сложные линейные задачи, создавать практически неограниченное количество библиотек пользовательских формул, констант и различных коэффициентов.
Страница
программы NumLock Calculator